[프로그래머스 알고리즘 스터디] 4주차 - 2 x n 타일링

YUZAMIN
YUZAMIN
Hello, World! I'm YUZAMIN, a diligently endeavoring frontend developer 🐤💦
[프로그래머스 알고리즘 스터디] 4주차 - 2 x n 타일링

Summary

문제 설명 📑

가로 길이가 2이고 세로의 길이가 1인 직사각형모양의 타일이 있습니다. 이 직사각형 타일을 이용하여 세로의 길이가 2이고 가로의 길이가 n인 바닥을 가득 채우려고 합니다. 타일을 채울 때는 다음과 같이 2가지 방법이 있습니다. -타일을 가로로 배치 하는 경우 -타일을 세로로 배치 하는 경우 직사각형의 가로의 길이 n이 매개변수로 주어질 때, 이 직사각형을 채우는 방법의 수를 return 하는 solution 함수를 완성해주세요.

제한사항 🚫

가로의 길이 n은 60,000이하의 자연수 입니다. 경우의 수가 많아 질 수 있으므로, 경우의 수를 1,000,000,007으로 나눈 나머지를 return해주세요.

문제 풀이 👩🏻‍💻

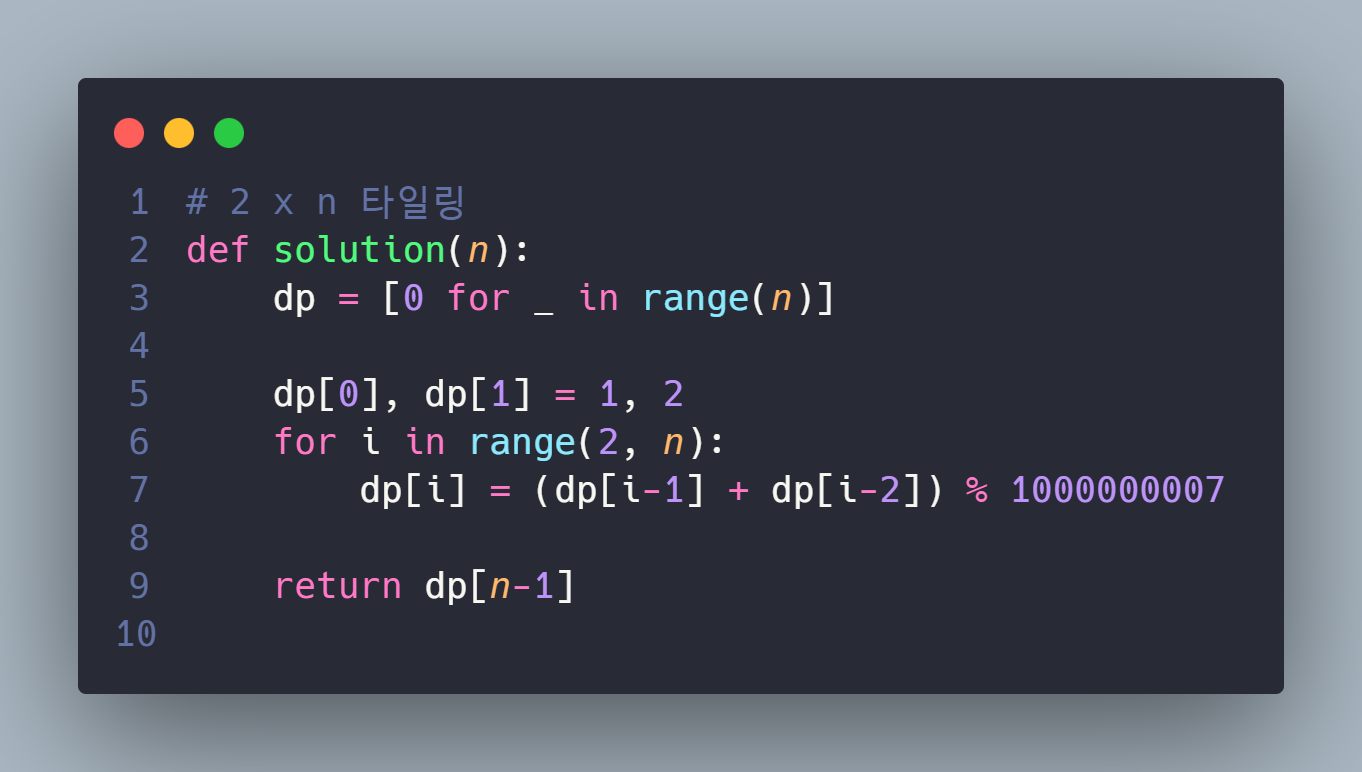
풀이

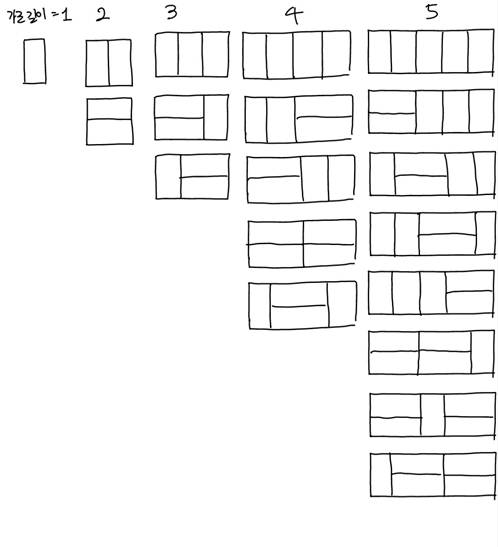
  • n = 5일 때 타일을 채울 수 있는 경우의 수 == n = 3일 때와 n = 4일 때 타일을 채울 수 있는 경우의 수의 합 (8 = 3 + 5)

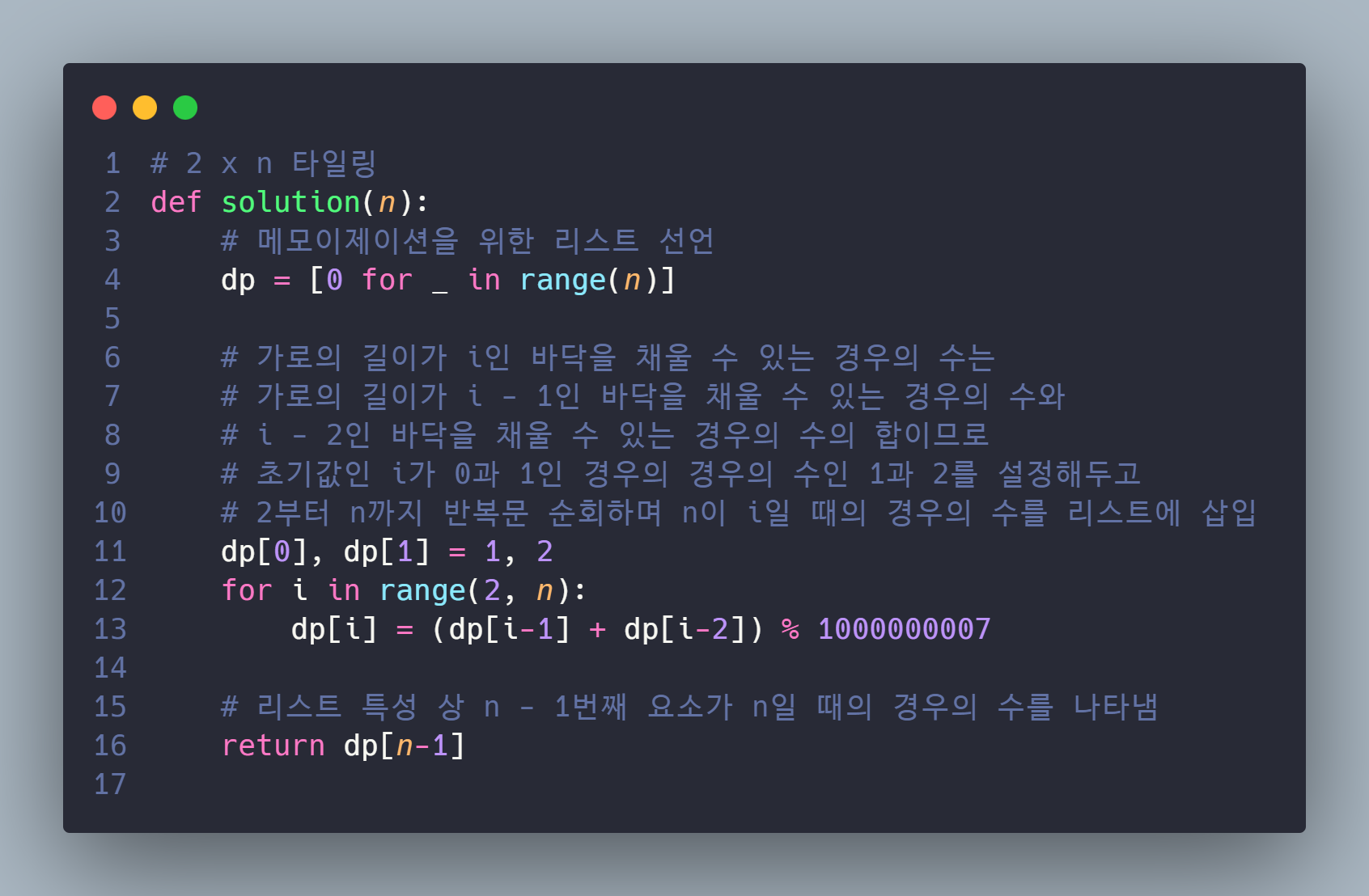
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

# 2 x n 타일링
def solution(n):
    # 메모이제이션을 위한 리스트 선언
    dp = [0 for _ in range(n)]

    # 가로의 길이가 i인 바닥을 채울 수 있는 경우의 수는
    # 가로의 길이가 i - 1인 바닥을 채울 수 있는 경우의 수와
    # i - 2인 바닥을 채울 수 있는 경우의 수의 합이므로
    # 초기값인 i가 0과 1인 경우의 경우의 수인 1과 2를 설정해두고
    # 2부터 n까지 반복문 순회하며 n이 i일 때의 경우의 수를 리스트에 삽입
    dp[0], dp[1] = 1, 2
    for i in range(2, n):
        dp[i] = (dp[i-1] + dp[i-2]) % 1000000007

    # 리스트 특성 상 n - 1번째 요소가 n일 때의 경우의 수를 나타냄
    return dp[n-1]

문제 출처